Introduction
Hey there ✋!
This article covers one of the projects on Binarized Neural Network (BNN), using the language of mathematical logic. Today we will explore:
- Maximum satisfiability problem statement
- Describing a Neural Network in terms of algebraic logic
- Comparison between BNN and Feed Forward Neural Network (FFNN) architecture in terms of CPU time and number of trainable parameters
- Drawbacks of Binarized Neural Networks
Please beware, that one is expected to have grounds in algebraic logic, to fully understand the concepts below. Otherwise, feel free to skip to the comparison section.
Problem statement
Binarized Neural Network (BNN) can be described in terms of a Maximum Satisfiability problem. Imagine, that we have a set of clauses (simply speaking, statements), involving logical variables. Weights w1, w2, … wn are assigned to these clauses C1, C2, … Cn. We need to find a combination of logical variables, such that the summary weight of all the satisfied clauses is maximal, while some of the clauses might not be satisfied. In other words, it is not compulsory, that the weights satisfy to all the clauses.
In addition, we introduce clauses D1, D2, … Dn, that must be satisfied (so-called hard clauses). This constitutes a problem of maximum satisfiability.

Neural Network in algebraic logic language
Since we work in terms of algebraic logic, all features and all weights of BNN network represent binary variables. Thus, an image below represents a simple BNN with the output layer of three neurons, and one output unit for a classification task. Note, that FFNN model uses scalar products between its weights and the features. Thus, the activation function of an output unit should be a step function, to map the scalar product into a binary logic output.
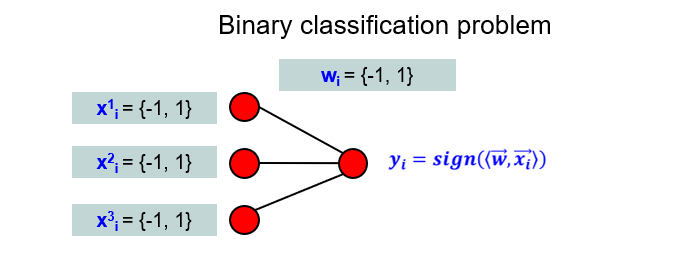
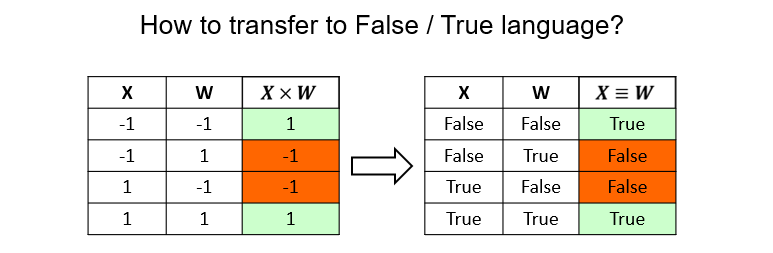
We know, that FFNN uses multiplication between features and weights. What we need is to find a substitute for a product, that comes from the realm of algebraic logic. It is an operation of equivalence. Indeed, from the tables below, you can make sure, that equivalence gives the same results as taking a product between the object features and weights.
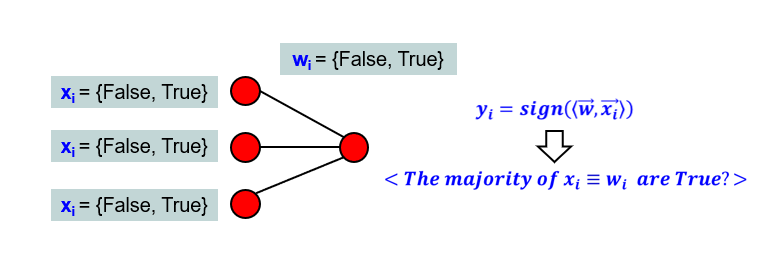
Now, this is time to adapt the activation of the output neuron to algebraic logic. We know, that sign(x) function is positive, provided that its argument is greater than zero.
Now imagine our output neuron computing the preactivation, which is to calculate all equivalences between features and corresponding weights (e.g. if feature x1 (which can be True or False) is equivalent to the weight w1 (which can be True or False), and so on). These equivalences can be True or False. Think of it like every True equivalence is adding +1 to preactivation, while every False equivalence is the same, as subtracting 1 from the preactivation.
Then, the sign(x) function will return a positive result, if majority of the equivalences between features x and weights w are True
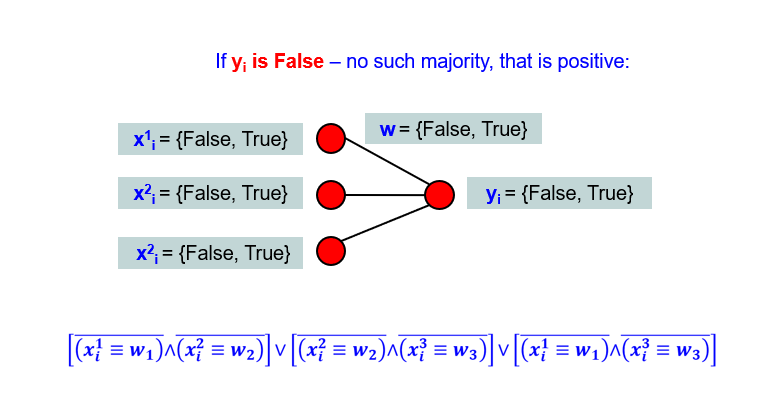
To sum up, the activation function of the BNN output neuron is a binary variable (True or False), that is an answer to a question: “Is the majority of the equivalences between features x and weights w evaluated to True?”
Training procedure
Imagine now, that we are working with one instance of the training dataset, xi, and the ground truth for xi is yi. Ground truth, in case of one output neuron, represents a binary variable, which can evaluate only to True or False (to stay compliant with the language of algebraic logic).
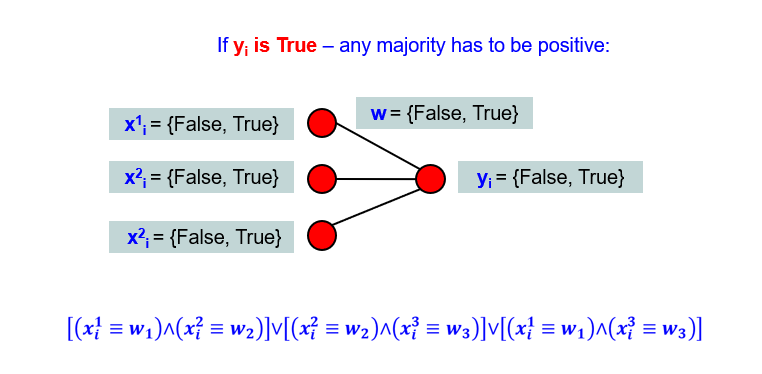
If yi is True, then the majority of the equivalences have to evaluate to True, so that the BNN output would be True as well. In case of three neurons in the input layer, that means that:
-
Whether first feature of xi is equivalent to the first weight w1 and second feature of xi is equivalent to the second weight w2
-
Or second feature of xi is equivalent to the second weight w2 and third feature of xi is equivalent to the third weight w3
-
Or first feature of xi is equivalent to the first weight w1 and third feature of xi is equivalent to the third weight w3
Do you see, that we simply recalled all the combinations of the majority? As simple as that! And in the language of disjunctive normal forms it will be written with the formula below:
In case when the ground truth yi is False, we want, that there is no such majority of True equivalences. This will be rewritten with the negation of the previous formula:
Essentially, training procedure is to utilize the algorithms that solve the maximum satisfiability problem (for example, the one used in this project is called Fu Malik). These algorithms will fine-tune the BNN weights. In other words, they will chose the False or True assignments, such that this combination of weights satisfies to as many instances of the dataset as possible. Or, if the dataset instances are weighted, the combination of BNN weight variables will satisfy the requirement of having the highest weighted sum of the correctly processed dataset instances. This is very intetersing to note, that BNN is a peculiar network, that does not use gradient back propagation.
But before we use these algorithms, we must convert the disjunctive normal forms into conjunctive normal forms!
To be honest, this is an extremely tedious process, even in the case of only three neurons! This has been automated in the code, but in the images below you can see, how to derive the conjunctive normal forms.



Experiments
For the experimental section, we introduce a shallow BNN with five neurons in the input layer and one output neuron. The ground truth function, that the BNN will learn, is to check, whether the second feature of the instance is True.
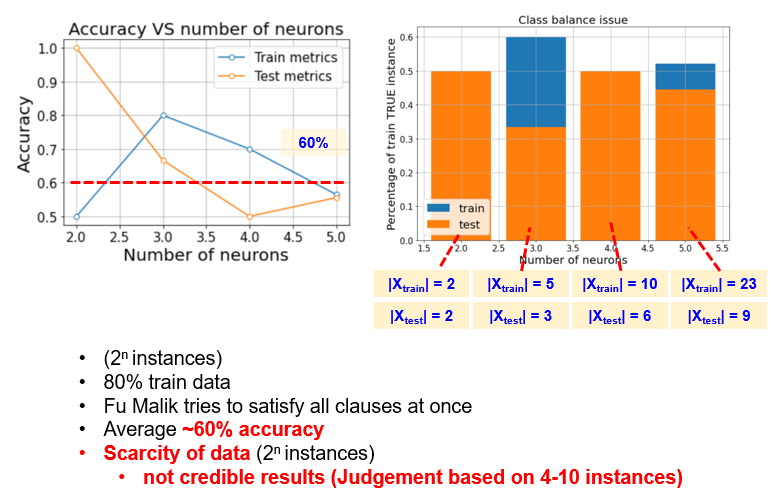
For the five neurons in the input layer, we have 32 unique instances, that were split into 25 training instances and 8 validation instances. As the first result, the model achieves 78% and 66% classification accuracy on training and validation datasets (please refer to the image below). I admit, that the results are pretty discouraging 🤔. Even maintaining the class balance did not improve the metric.

If we consider, how train and validation accuracies vary with number of input neurons, we will see, how much the metrics fluctuate from one to another. This is caused by the fact, that it is challenging to judge about the BNN performance, based on tiny datasets of less than 50 instances (please refer to the image below).
Weaknesses of Binarized Neural Networks
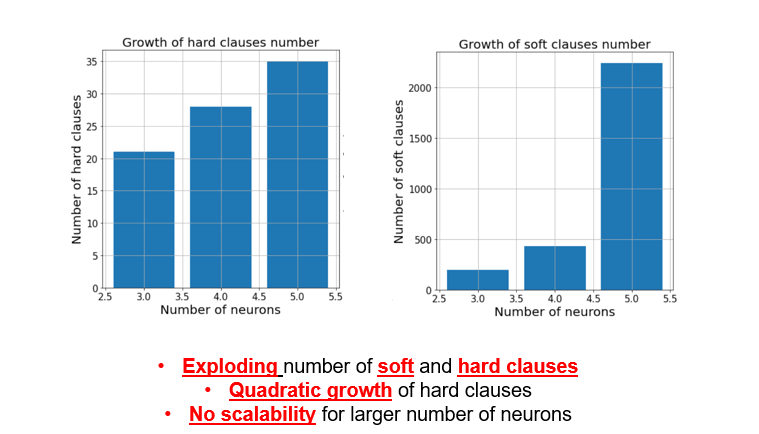
You might be wondering, why so few neurons? Why didn’t I test the deeper architectures, to improve the classification accuracy? This is due to the exponential explosion of the:
- Number of hard clauses for maximum satisfiability problem statement
- Number of soft clauses
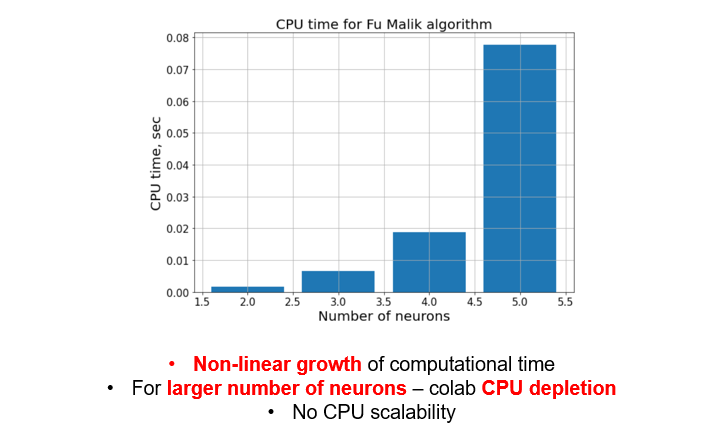
- CPU time to find the optimal weights of the network
You can see the details of the measurements in the image below. Indeed, with bigger architectures, I did not manage to finish training, as the CPU resources on Colab were totally depleted! Unfortunately, this makes binarized networks difficult to train and deploy for real world applications.
Comparison with Feed Forward Neural Network
To compare BNN and FFNN, we use the same FFNN architecture, which has one neuron more (bias neuron). We use five units in the input layer, and the dataset of 32 unique instances is split into 80% and 20% of the training and validation data respectively.
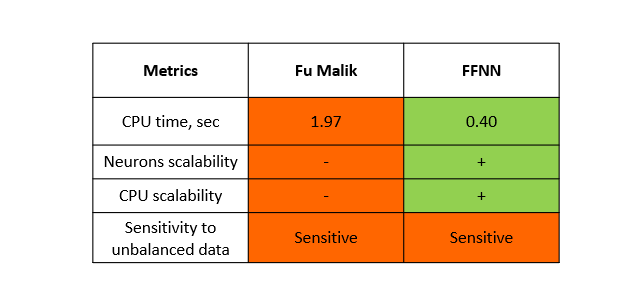
From the data below, you can see evident shortcomings of BNN as well - it requires much more CPU time, to learn even from the tiny datasets.
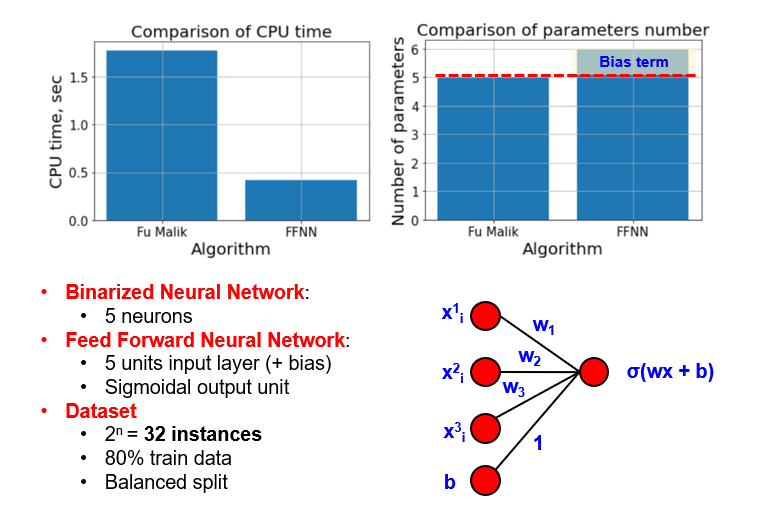
Conclusion
In this post, we’ve had a look at the Binarized Neural Networks. This is a specific architecture, that does not use gradient propagation methods for training. Instead, we describe neural network in terms of algebraic logic, and utilize Fu Malik algorithm to find optimal weights, that will suffice to as many training instances as possible.
However, this architecture is considerably worse than Feed Forward Neural Networks in terms of neurons scalability and CPU resources for training. This makes it challenging to achieve high performance with BNN model, therefore for now they are interesting only from academic point of view.